Pociąg i bandyta (kinematyka) gość44: 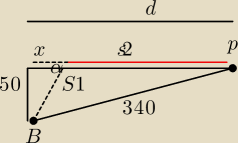Mam problem z takim oto zadaniem. Bandyta zaplanował napad na pociąg. Stoi on w odległości 50 metrów od prostego odcinka torów kolejowych i 340 m od czoła pociągu. Prędkość maksymalna bandyty wynosi 3m/s a pociąg porusza się z prędkością 15m/s. Trzeba ustalić w jakim kierunku musi iść bandyta by wskoczyć do lokomotywy i obliczyć najmniejszą prędkość z jaką musi biec by dogonić pociąg. Jeśli chodzi o kierunek to obliczyłem długość odcinka d = 336 m i założyłem, że S2=5S1 ( S2 = d −x), ponieważ prędkość pociągu jest 5 razy większa od prędkości bandyty i x=√S1²−2500 z Pitagorasa. Ostatecznie robię z tego równianie 336−√S1²−2500=5S1. Wychodzi mi równanie kwadratowe otrzymuje dwie różne drogi S1, jednak odpowiedzi są ostatecznie złe. Poprosiłbym o małą pomoc w tym zadaniu.

: wpisz w google już poradzono sobie z tym problemem na kilku stronach

gość44: Sprawdziłem i owszem takie zadanie było na tej stronie już 2 razy, lecz niestety w żadnym z nich nie ma ani nic konkretnego w odpowiedziach.

: to że znalazłeś coś tutaj, to cud, poszukaj gdzie indziej

: hint U{s₁}{v₁ = t = U{s₂}{v₂

	340 − x
√502 + x2 =
	5

dostajesz 2 rozwiazania, bo bandyta może biec w drugą stronę (w lewo) x ≈ 35 m

gość44: O, dziękuję bardzo.